Решение задачи #20. Python Яндекс CodeRun, Гистограмма и прямоугольник

Вариант решения задачи на языке программирования Python с Яндекс CodeRun.
Категория: Алгоритмы.
Название задачи: Гистограмма и прямоугольник.
Сложность: Средняя.
Статус решения: "Решено".

Условие задачи:
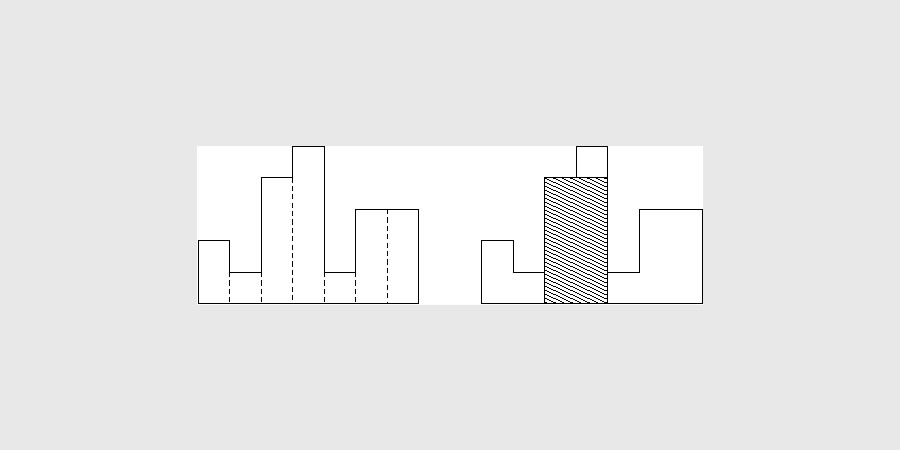
Гистограмма является многоугольником, сформированным из последовательности прямоугольников, выровненных на общей базовой линии. Прямоугольники имеют равную ширину, но могут иметь различные высоты. Например, фигура слева показывает гистограмму, которая состоит из прямоугольников с высотами 2, 1, 4, 5, 1, 3, 3. Все прямоугольники на этом рисунке имеют ширину, равную 1.

Обычно гистограммы используются для представления дискретных распределений, например, частоты символов в текстах. Отметьте, что порядок прямоугольников очень важен. Вычислите область самого большого прямоугольника в гистограмме, который также находится на общей базовой линии. На рисунке заштрихованная фигура является самым большим выровненным прямоугольником на изображенной гистограмме:

Решение:

Python

import sys

def largest_rectangle_area(heights):
    """
    Функция для вычисления площади самого большого прямоугольника в гистограмме.
    """
    stack = []  # Стек для хранения индексов
    max_area = 0  # Максимальная площадь
    index = 0  # Текущий индекс

    while index < len(heights):
        # Если стек пуст или текущая высота больше или равна высоте элемента на вершине стека
        if not stack or heights[index] >= heights[stack[-1]]:
            stack.append(index)  # Добавляем текущий индекс в стек
            index += 1
        else:
            # Высота прямоугольника определяется элементом на вершине стека
            top_of_stack = stack.pop()
            
            # Если стек пуст, ширина равна текущему индексу
            width = index if not stack else index - stack[-1] - 1
            
            # Вычисляем площадь и обновляем максимальную площадь
            max_area = max(max_area, heights[top_of_stack] * width)

    # Обрабатываем оставшиеся элементы в стеке
    while stack:
        top_of_stack = stack.pop()
        width = index if not stack else index - stack[-1] - 1
        max_area = max(max_area, heights[top_of_stack] * width)

    return max_area

def main():
    # Читаем входные данные
    input_data = sys.stdin.read().split()
    n = int(input_data[0])  # Количество прямоугольников
    heights = list(map(int, input_data[1:]))  # Высоты прямоугольников

    # Вычисляем и выводим максимальную площадь
    print(largest_rectangle_area(heights))

if __name__ == '__main__':
    main()
	

Объяснение кода

Основная идея:
Для нахождения площади самого большого прямоугольника мы используем стек. Он помогает эффективно находить ближайшие меньшие элементы слева и справа для каждого прямоугольника.

Логика работы:
Проходим по гистограмме, добавляя индексы в стек, пока текущая высота не меньше высоты на вершине стека.
Когда встречаем меньшую высоту, извлекаем индексы из стека, вычисляем ширину текущего прямоугольника и обновляем максимальную площадь. После прохода обрабатываем оставшиеся элементы в стеке.

Сложность алгоритма:
Временная сложность: O(n), так как каждый элемент добавляется и удаляется из стека ровно один раз.

Пространственная сложность: O(n), так как стек может содержать до n элементов.

Преимущества подхода:
Эффективное использование памяти и времени.
Простота реализации для больших данных.

Источник решения: hdhai.com